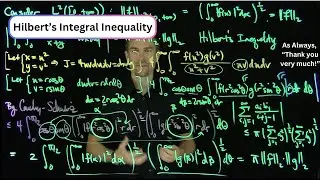Gibbs Phenomena
By considering the periodic sawtooth function, we show that the partial sums of its Fourier series have a first positive maximum value at pi/(n+1). The value of the partial sums at these maximal values converge as n tends to infinity to the sinc function integrated from zero to pi. Numerically, this is 9% more that the value of the jump at the origin. This is known as Gibbs Phenomena, and it is valid for functions which have a jump discontinuity in more generality. The partial sums of the Fourier series overcorrect for the jump discontinuity.
#mikethemathematician, #profdabkowski, #mikedabkowski
Watch video Gibbs Phenomena online, duration hours minute second in high quality that is uploaded to the channel Mike, the Mathematician 02 September 2024. Share the link to the video on social media so that your subscribers and friends will also watch this video. This video clip has been viewed 158 times and liked it 11 visitors.